 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
配点 : 900 点
問題文
あなたはカエル型のロボットを開発しています。 あなたはこのロボットに競走をさせることにしました。
まず、あなたは数直線上に N 体のロボットを置きました。 ロボットには 1 から N までの番号が振られています。 今、i 番目のロボットは座標 x_i にいます。 ただし、x_i はすべて整数であり、0 < x_1 < x_2 < ... < x_N が成り立ちます。
あなたは次の操作を繰り返し行います。
- 数直線上のロボットを一体選ぶ。 選んだロボットの座標を x とする。 座標 x - 1, x - 2 のうち他のロボットがいない座標を着地点に選ぶ。 選んだロボットを着地点へジャンプさせる。
あるロボットの座標が 0 以下になった場合、そのロボットはゴールしたと見なされ、即座に数直線から取り除かれます。 すべてのロボットがゴールするまで、あなたは操作を行い続けます。
あなたが操作を行う方法によって、N 体のロボットがゴールする順番は何通りかありえます。 N 体のロボットがゴールする順番は何通りありうるでしょうか? 10^9+7 で割った余りを求めてください。
制約
- 2 ≤ N ≤ 10^5
- x_i は整数である。
- 0 < x_1 < x_2 < ... < x_N ≤ 10^9
部分点
- 500 点分のテストケースでは、N ≤ 8 が成り立つ。
入力
入力は以下の形式で標準入力から与えられる。
N x_1 x_2 ... x_N
出力
N 体のロボットがゴールする順番は何通りありうるか? 10^9+7 で割った余りを出力せよ。
入力例 1
3 1 2 3
出力例 1
4
3 体のロボットがゴールする順番は、次の 4 通りありえます。
- (ロボット 1 → ロボット 2 → ロボット 3)
- (ロボット 1 → ロボット 3 → ロボット 2)
- (ロボット 2 → ロボット 1 → ロボット 3)
- (ロボット 2 → ロボット 3 → ロボット 1)
入力例 2
3 2 3 4
出力例 2
6
3 体のロボットがゴールする順番は、次の 6 通りありえます。
- (ロボット 1 → ロボット 2 → ロボット 3)
- (ロボット 1 → ロボット 3 → ロボット 2)
- (ロボット 2 → ロボット 1 → ロボット 3)
- (ロボット 2 → ロボット 3 → ロボット 1)
- (ロボット 3 → ロボット 1 → ロボット 2)
- (ロボット 3 → ロボット 2 → ロボット 1)
例えば、次図のように操作を行うと、(ロボット 3 → ロボット 2 → ロボット 1) の順にゴールします。
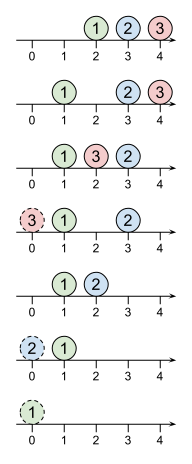
入力例 3
8 1 2 3 5 7 11 13 17
出力例 3
10080
入力例 4
13 4 6 8 9 10 12 14 15 16 18 20 21 22
出力例 4
311014372
答えを 10^9+7 で割った余りを出力してください。 なお、このケースは部分点のテストケースには含まれません。
Score : 900 points
Problem Statement
You are developing frog-shaped robots, and decided to race them against each other.
First, you placed N robots onto a number line. These robots are numbered 1 through N. The current coordinate of robot i is x_i. Here, all x_i are integers, and 0 < x_1 < x_2 < ... < x_N.
You will repeatedly perform the following operation:
- Select a robot on the number line. Let the coordinate of the robot be x. Select the destination coordinate, either x-1 or x-2, that is not occupied by another robot. The robot now jumps to the selected coordinate.
When the coordinate of a robot becomes 0 or less, the robot is considered finished and will be removed from the number line immediately. You will repeat the operation until all the robots finish the race.
Depending on your choice in the operation, the N robots can finish the race in different orders. In how many different orders can the N robots finish the race? Find the answer modulo 10^9+7.
Constraints
- 2 ≤ N ≤ 10^5
- x_i is an integer.
- 0 < x_1 < x_2 < ... < x_N ≤ 10^9
Partial Score
- In a test set worth 500 points, N ≤ 8.
Input
The input is given from Standard Input in the following format:
N x_1 x_2 ... x_N
Output
Print the number of the different orders in which the N robots can finish the race, modulo 10^9+7.
Sample Input 1
3 1 2 3
Sample Output 1
4
There are four different orders in which the three robots can finish the race:
- (Robot 1 → Robot 2 → Robot 3)
- (Robot 1 → Robot 3 → Robot 2)
- (Robot 2 → Robot 1 → Robot 3)
- (Robot 2 → Robot 3 → Robot 1)
Sample Input 2
3 2 3 4
Sample Output 2
6
There are six different orders in which the three robots can finish the race:
- (Robot 1 → Robot 2 → Robot 3)
- (Robot 1 → Robot 3 → Robot 2)
- (Robot 2 → Robot 1 → Robot 3)
- (Robot 2 → Robot 3 → Robot 1)
- (Robot 3 → Robot 1 → Robot 2)
- (Robot 3 → Robot 2 → Robot 1)
For example, the order (Robot 3 → Robot 2 → Robot 1) can be achieved as shown in the figure below:

Sample Input 3
8 1 2 3 5 7 11 13 17
Sample Output 3
10080
Sample Input 4
13 4 6 8 9 10 12 14 15 16 18 20 21 22
Sample Output 4
311014372
Remember to print the answer modulo 10^9+7. This case is not included in the test set for the partial score.