B - Row to Column Editorial /

Time Limit: 2 sec / Memory Limit: 256 MB

配点 : 1300 点

問題文

縦 N 行、横 N 列の正方形状のマス目があります。 上から i 行目、左から j 列目のマスを (i,\ j) と表します。

最初、各マスは白か黒です。 最初のマス目の配色は、正方形状に並ぶ文字 a_{ij} (1 ≤ i,\ j ≤ N) として与えられます。 マス (i,\ j) が白ならば a_{ij} は . であり、黒ならば a_{ij} は # です。

あなたは、マス目の配色を塗り替えるロボットを開発しています。 このロボットは次の操作を繰り返し行うことができます。

  • 整数 i, j (1 ≤ i,\ j ≤ N) をそれぞれ自由に選ぶ。 マス (i,\ 1), (i,\ 2), ..., (i,\ N) の色をそれぞれ c_1, c_2, ..., c_N として記憶する。 その後、マス (1,\ j), (2,\ j), ..., (N,\ j) の色をそれぞれ c_1, c_2, ..., c_N で塗り替える。

あなたの目標は、すべてのマスを黒にすることです。 すべてのマスを黒にすることが可能か判定し、可能ならば必要な操作回数の最小値を求めてください。

制約

  • 2 ≤ N ≤ 500
  • a_{ij} は . または # である。

部分点

  • 300 点分のテストケースでは、N ≤ 3 が成り立つ。

入力

入力は以下の形式で標準入力から与えられる。

N
a_{11}...a_{1N}
:
a_{N1}...a_{NN}

出力

すべてのマスを黒にすることが可能ならば、必要な操作回数の最小値を出力せよ。 不可能ならば、代わりに -1 を出力せよ。

入力例 1

2
#.
.#

出力例 1

3

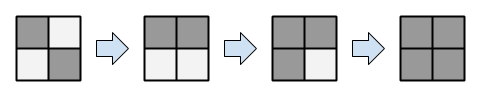
例えば、次のように操作を行うと、次図のようにマス目の配色が変わります。

  • i = 1, j = 2 と選んで操作を行う。
  • i = 1, j = 1 と選んで操作を行う。
  • i = 1, j = 2 と選んで操作を行う。
6a0314bb2b1073694a7ef5a062e77b13.png

入力例 2

2
..
..

出力例 2

-1

入力例 3

2
##
##

出力例 3

0

入力例 4

3
.#.
###
.#.

出力例 4

2

入力例 5

3
...
.#.
...

出力例 5

5

Score : 1300 points

Problem Statement

There is a square-shaped grid with N vertical rows and N horizontal columns. We will denote the square at the i-th row from the top and the j-th column from the left as (i,\ j).

Initially, each square is either white or black. The initial color of the grid is given to you as characters a_{ij}, arranged in a square shape. If the square (i,\ j) is white, a_{ij} is .. If it is black, a_{ij} is #.

You are developing a robot that repaints the grid. It can repeatedly perform the following operation:

  • Select two integers i, j (1 ≤ i,\ j ≤ N). Memorize the colors of the squares (i,\ 1), (i,\ 2), ..., (i,\ N) as c_1, c_2, ..., c_N, respectively. Then, repaint the squares (1,\ j), (2,\ j), ..., (N,\ j) with the colors c_1, c_2, ..., c_N, respectively.

Your objective is to turn all the squares black. Determine whether it is possible, and find the minimum necessary number of operations to achieve it if the answer is positive.

Constraints

  • 2 ≤ N ≤ 500
  • a_{ij} is either . or #.

Partial Score

  • In a test set worth 300 points, N ≤ 3.

Input

The input is given from Standard Input in the following format:

N
a_{11}...a_{1N}
:
a_{N1}...a_{NN}

Output

If it is possible to turn all the squares black, print the minimum necessary number of operations to achieve the objective. If it is impossible, print -1 instead.

Sample Input 1

2
#.
.#

Sample Output 1

3

For example, perform the operation as follows:

  • Select i = 1, j = 2.
  • Select i = 1, j = 1.
  • Select i = 1, j = 2.

The transition of the colors of the squares is shown in the figure below:

6a0314bb2b1073694a7ef5a062e77b13.png

Sample Input 2

2
..
..

Sample Output 2

-1

Sample Input 3

2
##
##

Sample Output 3

0

Sample Input 4

3
.#.
###
.#.

Sample Output 4

2

Sample Input 5

3
...
.#.
...

Sample Output 5

5